Question 56 3AE01 - Third Assistant Engineer

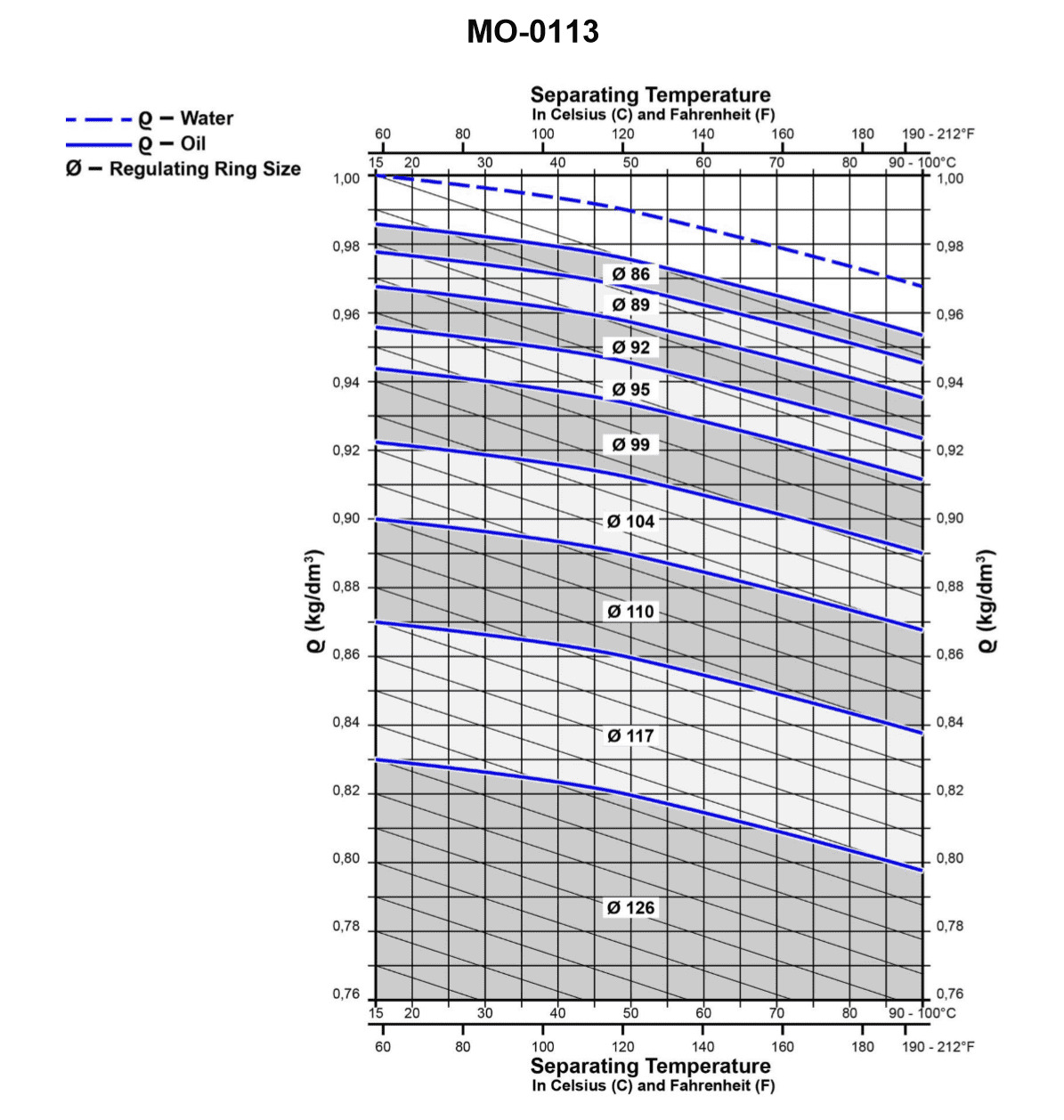
The Correct Answer is C ### Explanation for Option C (110 mm) The size of the regulating ring (gravity disc) required for a fuel oil centrifuge is determined by the specific gravity of the fuel oil at the separating temperature and the specific gravity of the water used (usually assumed to be 1.0 kg/dm³). This relationship is typically represented by a formula or, in practical operation, by a graph (such as Illustration MO-0113) which plots the required ring size against the specific gravity of the oil at the separation temperature. To solve this problem using the hypothetical Illustration MO-0113, we must first convert the given fuel oil specific gravity (S.G.) from the reference condition ($0.9 \text{ kg/dm}^3$ at $68^\circ\text{F}$) to the actual separating temperature ($158^\circ\text{F}$). 1. **Determine the Temperature Difference ($\Delta T$):** $$\Delta T = \text{Separating Temperature} - \text{Reference Temperature}$$ $$\Delta T = 158^\circ\text{F} - 68^\circ\text{F} = 90^\circ\text{F}$$ 2. **Estimate the Change in Specific Gravity:** Specific gravity decreases as temperature increases. For typical marine fuel oils, the specific gravity changes by approximately $0.00065$ per $1^\circ\text{C}$ (or $0.00036$ per $1^\circ\text{F}$). $$\text{S.G. change} = 90^\circ\text{F} \times 0.00036 \text{ /}^\circ\text{F} \approx 0.0324 \text{ kg/dm}^3$$ 3. **Calculate Specific Gravity at Separating Temperature ($\text{S.G.}_{\text{sep}}$):** $$\text{S.G.}_{\text{sep}} = \text{S.G.}_{\text{ref}} - \text{S.G. change}$$ $$\text{S.G.}_{\text{sep}} = 0.900 \text{ kg/dm}^3 - 0.0324 \text{ kg/dm}^3 \approx 0.868 \text{ kg/dm}^3$$ 4. **Use Illustration MO-0113:** Assuming Illustration MO-0113 is a standard graph for determining gravity disc size based on the oil's specific gravity at separation temperature: * Locate the calculated $\text{S.G.}$ of $0.868 \text{ kg/dm}^3$ on the x-axis (Specific Gravity). * Follow this value up to the curve representing the required regulating ring diameter. * Read the corresponding diameter on the y-axis (Ring Diameter). For an $\text{S.G.}_{\text{sep}}$ of approximately $0.868$, a standard centrifuge graph shows that the required regulating ring size is $110 \text{ mm}$. *** ### Explanation of Why Other Options Are Incorrect **A) 86 mm:** A regulating ring size of $86 \text{ mm}$ corresponds to a much higher specific gravity oil, typically around $0.94$ to $0.95 \text{ kg/dm}^3$. Since the calculated specific gravity at separation is $0.868 \text{ kg/dm}^3$, this disc is far too small and would lead to the separation zone moving inward, likely causing the oil/water interface to be pushed into the oil overflow, resulting in oil loss (sludging of oil). **B) 104 mm:** A ring size of $104 \text{ mm}$ corresponds to a specific gravity closer to $0.88$ or $0.89 \text{ kg/dm}^3$. While closer than Option A, it is still smaller than required for an $\text{S.G.}$ of $0.868 \text{ kg/dm}^3$. This disc would also be slightly too small, potentially leading to operational instability and inefficient separation, or even oil loss if the gravity boundary shifts too far inward. **D) 117 mm:** A ring size of $117 \text{ mm}$ corresponds to a very low specific gravity oil, typically below $0.85 \text{ kg/dm}^3$. This disc is too large for the calculated specific gravity of $0.868 \text{ kg/dm}^3$. If a disc that is too large is used, the oil/water interface moves outward, increasing the risk of the interface being pushed into the sludge space, causing the water seal to break and water to exit with the clean oil (water contamination).