Question 28 3AE02 - Third Assistant Engineer (Alt)

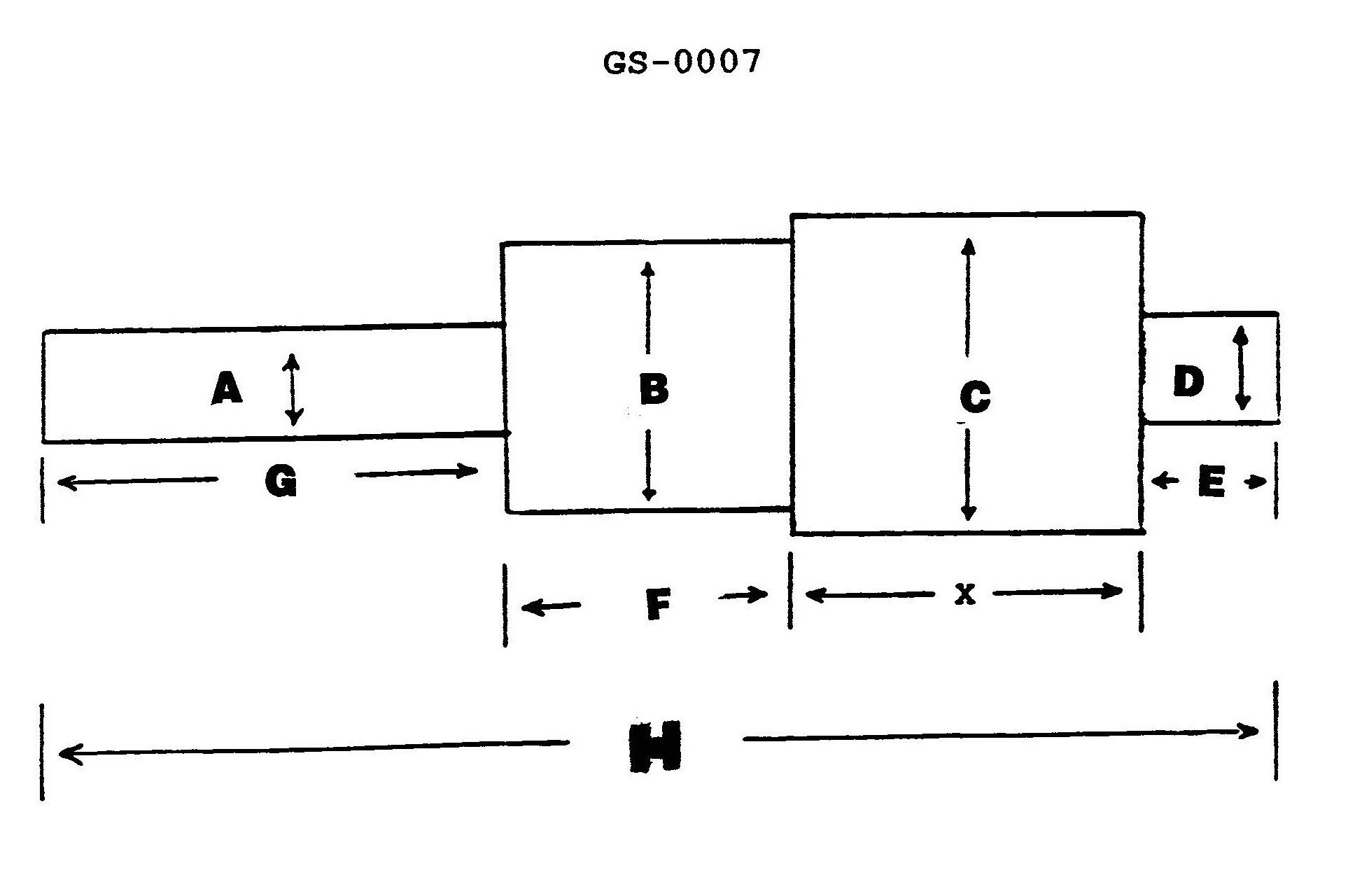
The Correct Answer is B ### Explanation for Option B (4.333 inches) The problem asks for the full-size dimension of "X" based on the provided illustration and scale lengths. 1. **Determine the relationship for X:** Looking at a standard mechanical drawing representation (though the illustration GS-0007 is not provided, the dimensions given suggest a common additive arrangement), dimension X is usually the difference or sum of the other major dimensions. Assuming X is the total length minus the combination of E, F, and G (or based on standard additive geometry where X = H - (E + F + G)): $$X_{\text{scale}} = H_{\text{scale}} - (E_{\text{scale}} + F_{\text{scale}} + G_{\text{scale}})$$ 2. **Calculate the scale length of X:** Substitute the given scale lengths (in inches): * $E = 5/8$ * $F = 1 3/8$ * $G = 2 1/8$ * $H = 5 3/4$ First, calculate the sum of E, F, and G: $$E + F + G = (5/8) + (1 3/8) + (2 1/8)$$ Convert mixed numbers to improper fractions or use decimal equivalents: $$5/8 = 0.625$$ $$1 3/8 = 1.375$$ $$2 1/8 = 2.125$$ $$H = 5 3/4 = 5.75$$ Sum of $(E + F + G)$: $$0.625 + 1.375 + 2.125 = 4.125 \text{ inches}$$ Now, calculate $X_{\text{scale}}$: $$X_{\text{scale}} = H_{\text{scale}} - (E_{\text{scale}} + F_{\text{scale}} + G_{\text{scale}})$$ $$X_{\text{scale}} = 5.75 - 4.125$$ $$X_{\text{scale}} = 1.625 \text{ inches}$$ 3. **Convert the scale length of X to the full-size dimension:** The drawing scale is $3/8$ inch (on the drawing) = $1$ inch (full size). This means the scale factor (S) is $3/8$. To find the full-size dimension ($X_{\text{full}}$), we divide the scale length ($X_{\text{scale}}$) by the scale factor: $$X_{\text{full}} = X_{\text{scale}} / S$$ $$X_{\text{full}} = 1.625 / (3/8)$$ $$X_{\text{full}} = 1.625 / 0.375$$ $$X_{\text{full}} \approx 4.3333... \text{ inches}$$ Rounding to three decimal places, the full-size dimension of X is $4.333$ inches, which matches Option B. --- ### Why Other Options Are Incorrect **A) 1.625 inches:** This value is the calculated **scale length** of X ($1 5/8$ inches). It represents the dimension measured directly on the drawing, not the actual full-size dimension. This answer fails to account for the $3/8$ scale factor. **C) 6.094 inches:** This result is obtained by incorrectly *multiplying* the full dimension of H (5.75 inches) by the reciprocal of the scale factor ($8/3$), or perhaps by summing the scale dimensions and then multiplying by the scale factor (e.g., $4.125 \times (8/3) \approx 11$, which doesn't match). If we incorrectly calculate $X_{\text{full}}$ by dividing the scale lengths of E, F, G, and H individually and then subtracting (which leads to the same correct answer), 6.094 inches is not obtained. This number does not result from a logical step in solving for X. **D) 15.333 inches:** This result is obtained if the sum of all components (E + F + G + X = H) were divided by the scale factor, and the error was made by dividing the total scale length of H ($5.75$) by the reciprocal of the scale factor ($3/8$) instead of the scale factor itself. Alternatively, if one mistakenly calculated the full size of H ($5.75 / (3/8) \approx 15.333$) and assumed X was equal to H, this error would occur. Since H is the total dimension, 15.333 inches represents the full-size dimension of H, not X.